高精度模拟计算，北京大学取得重大进展

矩阵方程求解是线性代数的核心内容，在信号处理、科学计算及神经网络二阶训练等领域具有广泛应用。相较于常规矩阵乘法，矩阵求逆操作对输入误差的敏感性显著更高，因此对计算精度提出了严格要求。然而，采用数字方法实现高精度矩阵求逆的计算开销极大，其时间复杂度可达立方级。随着大数据驱动类应用的兴起，这种高复杂度计算给传统数字计算机带来了严峻挑战，尤其在传统器件尺寸缩放逼近物理极限、传统冯·诺依曼架构面临“内存墙”瓶颈的双重背景下，这一问题日益凸显。

在这一算力瓶颈的背景下，模拟计算因其通过物理定律直接实现高并行、低延时、低功耗运算的先天优势，重新进入研究视野。然而，传统模拟计算受限于低精度、难扩展等固有缺点，逐渐被高精度、可编程的数字计算所取代，成为存于教科书中的“老旧技术”。

基于阻变存储器阵列的模拟矩阵计算技术，被视为有望解决上述难题的路径之一。特别是基于“阵列-运算放大器”闭环反馈原理设计的矩阵求逆电路，能够实现矩阵求逆的一步式求解。尽管此类电路具备高速、高能效的计算潜力，但其固有的低精度特性仍是关键瓶颈，同时电路的硬连接结构也对其可扩展性构成挑战。此外，在模拟矩阵乘法计算中，可通过比特切片、模拟补偿等策略提升计算精度，也可通过将分块子矩阵映射至多个阵列的方式实现扩展性。然而，矩阵方程求解过程缺乏有效的分配律与分块矩阵方法支撑，这使得模拟矩阵求逆的精度与可扩展性问题长期未能得到有效解决。

当前，部分基于数模混合迭代的研究方案仍存在明显局限：一方面，此类方案虽可借助浮点数字计算机实现高精度残差计算，却大幅削弱了模拟计算在降低复杂度方面的核心优势，同时还需频繁执行模数转换操作；另一方面，现有模拟矩阵求逆电路的实验验证规模仍局限于小规模场景，且所用器件缺乏可靠的多级存储特性。

在这一背景下，北京大学集成电路学院、人工智能研究院研究团队在国际上首次实现了基于阻变存储器的高精度、可扩展模拟矩阵计算芯片，实现了在精度上可与数字计算媲美的模拟计算系统，将传统模拟计算的精度提升了五个数量级。相关性能评估表明，该芯片在求解大规模MIMO信号检测等关键科学问题时，计算吞吐量与能效较当前顶级数字处理器（GPU）实现大幅提升，为后摩尔时代应对人工智能与6G通信等领域的算力挑战开辟了全新路径。

图1 研究背景：模拟矩阵计算电路求解矩阵方程。

在这项工作中，研究团队选择了一条融合创新的道路，构建了一个基于阻变存储器阵列的高精度、可拓展的全模拟矩阵方程求解器。通过新型信息器件、原创电路和经典算法的协同设计，首次将模拟计算的精度提升至24位定点精度。

研究团队基于迭代算法，结合了模拟低精度矩阵求逆和模拟高精度矩阵-向量乘法运算，开发了一种基于全模拟矩阵运算的高精度矩阵方程求解方案（图2）。其中，模拟低精度矩阵求逆和模拟高精度矩阵-向量乘法运算保持了模拟矩阵计算固有的低复杂度。特别需要注意的是，模拟矩阵求逆有助于减少迭代次数，因为该方法可以在每次迭代中提供近似正确的结果。而高精度模拟MVM通过位切片方法，实现迭代细化过程。

此外，模拟低精度矩阵求逆和模拟高精度矩阵-向量乘法运算两个电路的阻变存储器阵列在40nm CMOS工艺平台制造，可实现3比特电导态编程。

图2 高精度全模拟矩阵计算求解矩阵方程。

通过与块矩阵算法相结合，研究团队在实验上成功实现了16×16矩阵的24比特定点数精度求逆（图3）。具体而言，矩阵方程求解经过10次迭代后，相对误差可低至10⁻⁷量级，展现了该方案在计算精度上的显著优势。

在应用验证层面，该方法被成功应用于大规模多输入多输出（MIMO）系统的信号检测任务。研究团队展示了基于迫零检测的图像恢复效果，在第二个迭代周期内，接收图像即与原始图像达到高度一致。进一步的误码率-信噪比分析显示，仅需三次迭代，该系统在无线通信场景下的检测性能即可媲美32位浮点精度数字处理器（图4），凸显出其在实时信号处理中的潜力。

综合基准测试结果证实，在保持相当计算精度的前提下，本模拟计算方法可实现领先的处理速度和能效（图5）。这些成果不仅验证了全模拟矩阵求解路径的可行性，也为应对未来智能计算与通信系统中的算力瓶颈提供了具有前景的技术平台。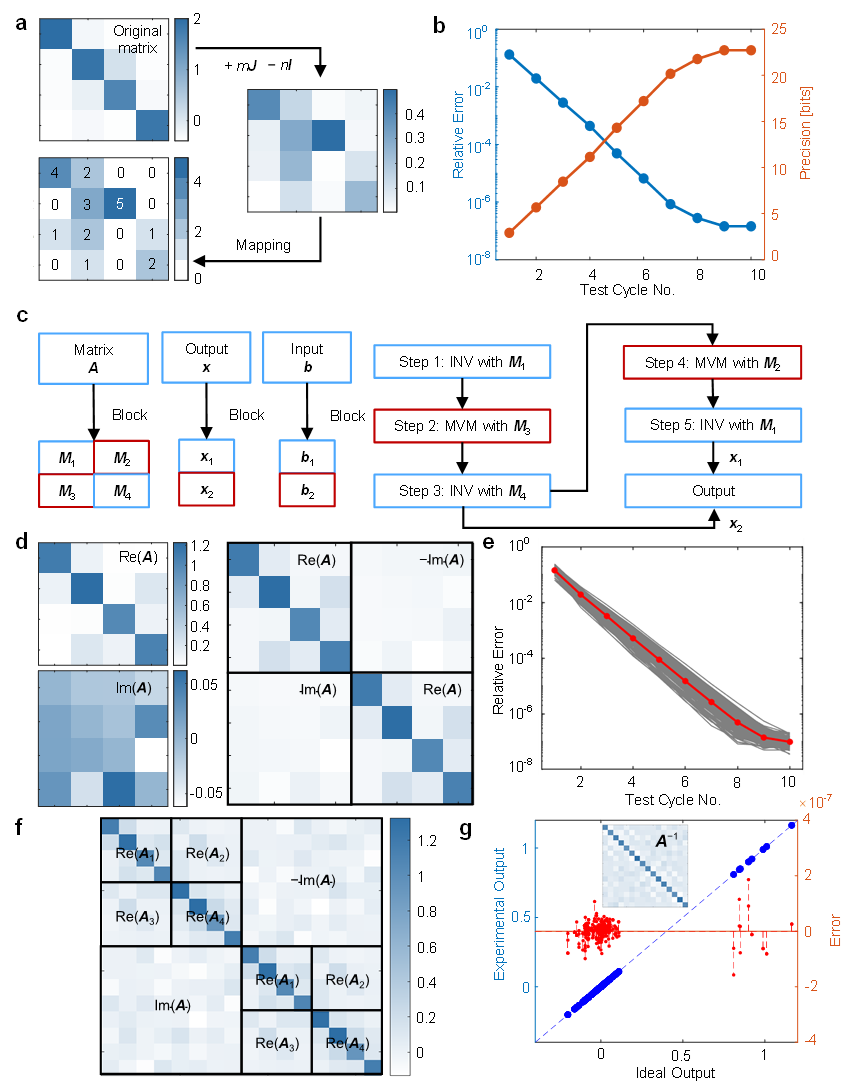
图3 基于块矩阵方法求解高精度、可拓展矩阵方程的实验结果

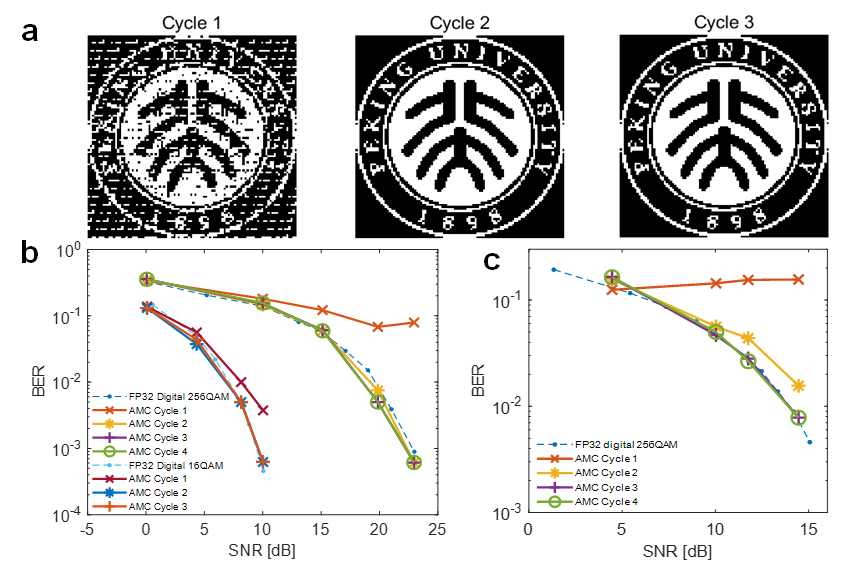
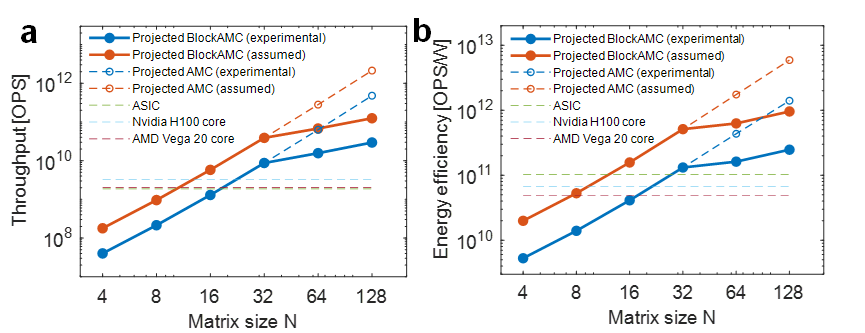图4 高精度矩阵方程求解在大规模多输入多输出（MIMO）迫零检测信号处理过程中的应用。图5 模拟矩阵计算求解的性能比较（计算精度均为FP32精度）。
相关成果以《Precise and scalable analogue matrix equation solving using resistive random-access memory chips》为题，发表于国际顶级期刊《自然·电子学》（Nature Electronics）。论文共同第一作者为集成电路学院、人工智能研究院博士生左濮深与集成电路学院博士毕业生王錡深，通讯作者为人工智能研究院与集成电路学院联聘研究员孙仲，以及集成电路学院蔡一茂教授、王宗巍研究员。该研究得到了国家自然科学基金、国家重点研发计划的支持。

论文链接：https://www.nature.com/articles/s41928-025-01477-0