仅凭AI不足以进行芯片设计

自1971 年Federico Faggin仅用直尺和彩色铅笔绘制出第一款商用微处理器Intel 4004以来，芯片设计已经取得了长足的进步。如今的设计师拥有大量软件工具来规划和测试新的集成电路。但随着芯片变得异常复杂（有些芯片包含数千亿个晶体管），设计师必须解决的问题也随之增加。而这些工具并不总是能胜任这项任务。

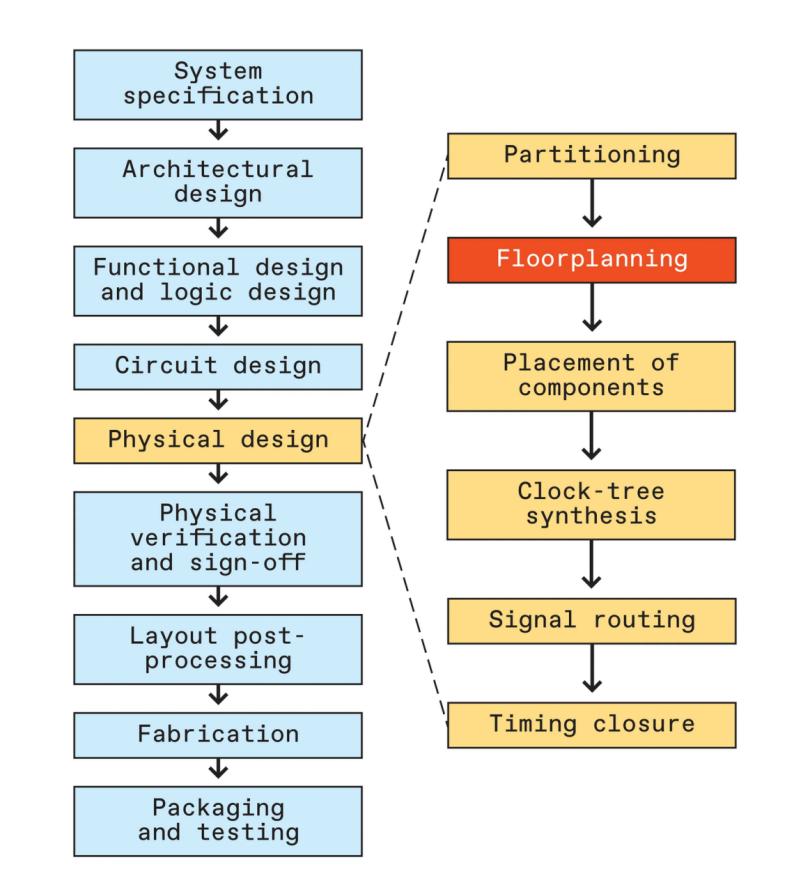
现代芯片工程是一个由九个阶段组成的迭代过程，从系统规范到 封装。每个阶段都有几个子阶段，每个阶段可能需要数周到数月的时间，具体取决于问题的规模及其约束。许多设计问题只有少数几个可行解决方案。当今使用的自动化工具通常无法解决这种规模的实际问题，这意味着必须由人类介入，这使得该过程比芯片制造商所希望的更加费力和耗时。

人们对使用机器学习来加速芯片设计的兴趣日益浓厚 。然而，正如英特尔人工智能实验室的团队所发现的那样，机器学习算法本身往往是不够的，特别是在处理必须满足的多个约束时。

事实上，研究者最近尝试开发一种基于人工智能的解决方案来解决一项棘手的设计任务，即布局规划（稍后会详细介绍这项任务），这让他们开发出了一种基于非人工智能方法（如传统搜索）的更为成功的工具。这表明该领域不应过早放弃传统技术。

人工智能算法的危险

芯片设计中最大的瓶颈之一出现在物理设计阶段，即在确定架构、设计逻辑和电路之后。物理设计涉及对芯片布局和连接进行几何优化。第一步是将芯片划分为高级功能块，例如 CPU 内核、内存块等。然后，这些大分区被细分为较小的分区，称为宏和标准单元。一个普通的片上系统 (SoC) 有大约 100 个高级块，由数百到数千个宏和数千到数十万个标准单元组成。

接下来是布局规划，其中功能块的排列是为了满足某些设计目标，包括高性能、低功耗和成本效益。这些目标通常通过最小化线长（连接电路元件的纳米线的总长度）和空白区域（未被电路占用的芯片总面积）来实现。此类布局规划问题属于数学编程的一个分支，称为组合优化。

芯片布局规划就像是强化版的俄罗斯方块。首先，可能的解决方案数量可能大到天文数字——确实如此。在典型的 SoC 布局规划中，排列 120 个高级块的可能方法大约有 10 250种。宏和标准单元的可能排列数量则要大几个数量级。

给定一个目标（例如将功能块压缩到尽可能小的硅片面积中），商用布局规划工具可以在几分钟内解决如此规模的问题。然而，当面临多个目标和约束时，它们就会陷入困境，例如关于某些块必须放在哪里、它们如何成形或哪些块必须放在一起的规则。

尽管过去十年机器学习 取得了巨大成功，但迄今为止它对芯片设计的影响相对较小。Nvidia 等公司已经开始 训练大型语言模型(LLM)（支持 Copilot 和 ChatGPT 等服务的 AI 形式），以编写硬件设计程序脚本并分析错误。但这些编码任务与解决布局规划等棘手的优化问题相去甚远。

乍一看，将 变压器模型（LLM的基础）也用于物理设计问题可能也很诱人。理论上，科学家可以通过训练变压器来按顺序预测芯片上每个块的物理坐标，从而创建基于 AI 的布局规划器，类似于 AI 聊天机器人按顺序预测句子中的单词的方式。但是，如果试图教模型将块放置在不重叠的位置，那么很快就会遇到麻烦。虽然对于人类来说很容易理解，但对于计算机来说，学习这个概念并不容易，因此需要大量的训练数据和时间。对于进一步的设计约束也是如此，例如将块放置在一起或靠近某个边缘的要求。

因此，研究者采取了不同的方法。首要任务是选择一种有效的数据结构来传达平面图中块的位置。研究者选择了所谓的 B* 树。在这个结构中，每个块都表示为二叉树上的一个节点。平面图左下角的块成为根。右侧的块成为一个分支；顶部的块成为另一个分支。每个新节点都延续此模式。因此，随着树的增长，它会在向右和向上扇形扩展时封装平面图。

B* 树结构的一大优势是它保证了无重叠的布局规划，因为块位置是相对的而不是绝对的——例如，“在另一个块上方”而不是“在这个位置”。因此，AI 布局规划器不需要预测它放置的每个块的确切坐标。

有了数据结构后，研究者在包含数百万个最优布局规划的数据集上训练了几种机器学习模型，具体来说，是图神经网络、扩散模型和基于变压器的模型。这些模型学会了预测放置在先前放置的块上方或右侧的最佳块，以生成针对面积和线长进行了优化的布局规划。但很快意识到这种循序渐进的方法是行不通的。研究者将布局规划问题扩展到大约 100 个块，并在无重叠规则之外添加了硬约束。这些包括要求将一些块放置在预定位置（如边缘）或对共享同一电压源的块进行分组。

问题在于模型无法回溯：由于它们按顺序放置积木，因此无法追溯之前的错误放置。研究者可以使用强化学习代理等技术来绕过这个障碍，但这种代理训练一个好的模型所需的探索量是不切实际的。

回归芯片设计传统

解决大规模组合优化问题的一种常用方法是使用一种称为模拟退火(SA) 的搜索技术 。模拟退火于 1983 年首次提出，其灵感来自冶金学，其中退火是指将金属加热到高温然后缓慢冷却的过程。通过控制能量的减少，原子可以有序排列，使材料比快速冷却时更坚固、更柔韧。以类似的方式，模拟退火可以逐步找到优化问题的最佳解决方案，而无需繁琐地检查每种可能性。

它的工作原理如下。算法从随机解决方案开始 — 就目的而言，随机布局规划表示为 B* 树。然后，我们允许算法采取以下三种操作之一，同样是随机的：它可以交换两个块、将一个块从一个位置移动到另一个位置，或者调整一个块的宽高比（不改变其面积）。我们通过对总面积和线长取加权平均值来判断最终布局规划的质量。这个数字描述了操作的“成本”。

然而，随着时间的推移，随着算法不断随机调整块，研究者接受增加成本的操作的频率会越来越低。就像在金属加工中一样，他们希望逐步实现这种转变。就像过快冷却金属会使其原子陷入无序排列一样，过早限制算法的探索会使其陷入次优解决方案，即局部最小值。通过给算法足够的回旋余地来尽早避开这些陷阱，也可以诱导它走向我们真正想要的解决方案：全局最小值（或它的良好近似值）。

相比使用任何机器学习模型，利用 SA 解决布局规划问题的成功率要高得多。由于 SA 算法没有布局顺序的概念，因此它可以随时更改任何块，本质上允许算法纠正先前的错误。在没有限制的情况下，它可以在几分钟内解决包含数百个块的复杂布局规划。相比之下，使用商业工具的芯片设计师需要数小时才能解决同样的难题。

当然，现实世界的设计问题有限制。因此，研究者为 SA 算法提供了一些与机器学习模型相同的限制，包括对某些块的放置位置和分组方式的限制。他们首先尝试通过将布局违反这些限制的次数添加到我们的成本函数中来解决这些硬约束。现在，当算法进行随机块更改以增加约束违反时，会以更高的概率拒绝这些操作，从而指示模型避免这些操作。

但不幸的是，这种策略适得其反。在成本函数中包含约束意味着算法将尝试在满足约束和优化面积和线长之间找到平衡。但根据定义，硬约束是不能妥协的。然而，当他们增加约束变量的权重来解释这种刚性时，算法在优化方面表现不佳。模型没有努力修复导致全局最小值（最佳布局规划）的违规行为，而是反复导致模型无法摆脱的局部最小值（次优布局规划）。